Schriftlich Geteilt Rechnen Mit Komma

Geschrieben von: Dennis Rudolph
Sonntag, 28. Februar 2021 um 11:11 Uhr

Das schriftliche Dividieren mit Komma sehen wir uns in den nächsten Abschnitten an. Dies bekommt ihr erklärt:

• Eine Erklärung, wie das schriftliche Dividieren mit Kommazahlen funktioniert.
• Einige Beispiele zur Verdeutlichung.
• Aufgaben / Übungen damit ihr das Thema selbst ein bisschen üben könnt.
• Ein Video zum schriftlichen Dividieren .
• Ein Frage- und Antwortbereich zu diesem Thema.

Wir sehen uns gleich das schriftliche Dividieren mit Komma an. Es ist nicht zwingend erforderlich das ihr bereits schriftlich Dividieren könnt, aber schaden tut es auch nicht. Wer mag kann also gerne noch in den Artikel schriftlich Dividieren Grundschule / 4. Klasse reinsehen. Alle anderen können gleich hier weitermachen.

Erklärung schriftlich Dividieren mit Kommazahlen

Zunächst ein kurzer Hinweis: Das schriftliche Dividieren mit Komma wird auch als schriftliches Dividieren mit Dezimalzahlen bezeichnet. Es gibt mehrere Möglichkeiten wo das Komma stehen kann und im Prinzip können auch zwei Kommas vorkommen.

Das schriftliche Dividieren mit Komma soll zunächst für 69,three : 3 gezeigt werden. Im Ergebnis setzen wir ein Komma sobald wir dieses bei der Berechnung erreichen. Dies schreiben wir uns als Aufgabe hin:

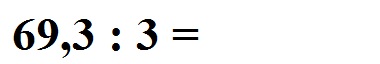
Wir haben ganz vorne eine 6 stehen. Geteilt wird durch eine iii. Wir müssen uns nun überlegen, wie often die 3 in die 6 geht. Dies geht two mal. Daher schreiben wir dice two in das Ergebnis.

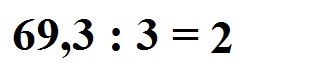
In die entgegengesetzte Richtung multiplizieren wir mit 2 · 3 = 6. Diese 6 schreiben wir unter die bereits vorhandene 6 vorne.

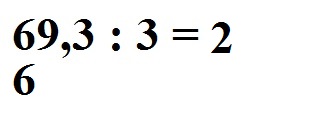
Nun müssen wir subtrahieren: 6 - six = 0. Dies schreiben wie so hin:

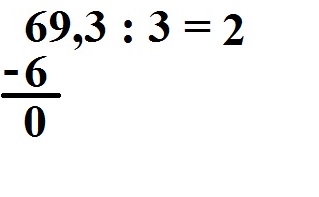
Wir ziehen die nächste Stelle von oben runter. Diese ist eine ix. Wir schreiben sie hinter die 0.

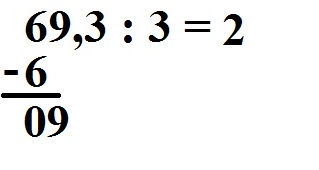
Wie ofttimes geht nun die 3 in dice nine? Dies geht 3 mal. Wir schreiben dice 3 in unser Ergebnis.

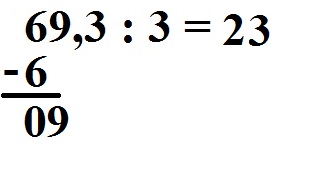
Wir multiplizieren wieder zurück: 3 · 3 = ix

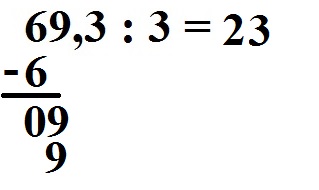
Wir subtrahieren wieder: 09 - 9 = 0.

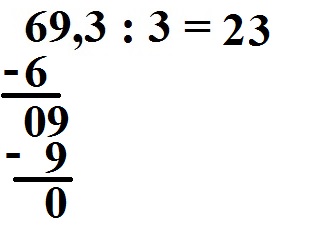
Jetzt erreichen wir das Komma. Daher setzen wir jetzt das Komma auch im Ergebnis.

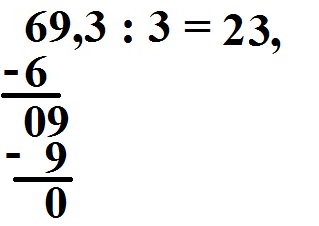
Wir ziehen die nächste Stelle nach unten. Dies wäre noch die iii.

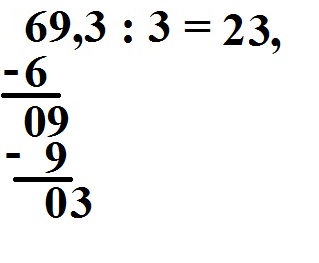
Nun wieder in die andere Richtung: Wie frequently geht die 3 in die iii rein? Dies geht 1 mal. Wir schreiben noch die 1 ins Ergebnis.

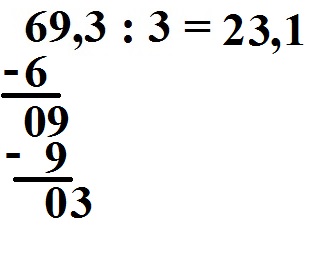
Wir multiplizieren wieder zurück: 1 · 3 = 3. Diese 3 schreiben wir unter die 03.

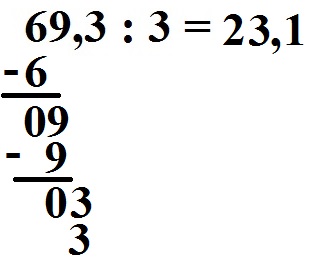
Wir subtrahieren ein letztes Mal. Mit 03 - 3 kommen wir auf eine 0.

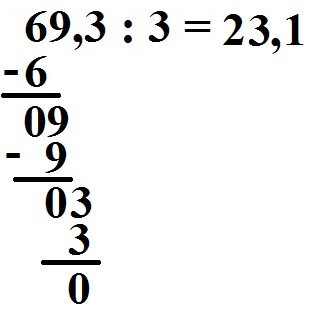
Wir haben eine 0 herausbekommen und keine weitere Stelle mehr zum runterziehen. Mit 23,1 haben wir das Ergebnis fertig berechnet.

Anzeige:

Beispiele schriftlich Dividieren mit Komma

Sehen wir uns einige weitere Beispiele zum schriftlichen Dividieren mit Kommazahlen an.

Beispiel 1:

Im nächsten Beispiel hat der Divisor - also die zweite Zahl - ein Komma. Berechnet weden soll 672 : v,half dozen. Wie lautet das Ergebnis?

Lösung:

Hier gibt es einen ganz einfachen Trick. Wir haben

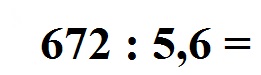
und multiplizieren dies einfach mit 10. Dadurch fliegt das Komma raus:

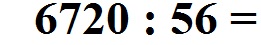
Wir können die Aufgabe nun so berechnen, wie homo dies von der schriftlichen Division ohne Komma her kennt. Zunächst die Rechnung, im Anschluss wird diese noch einmal in Kurzform erläutert.

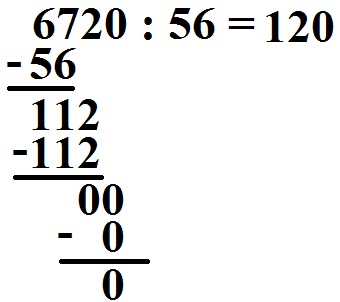
And so wurde gerechnet:

• Die six ganz vorne ist kleiner als die 56, daher nehmen wir die zweite Stelle noch dazu.
• Wir beginnen somit mit der 67.
• Die 56 geht in die 67 genau 1 mal rein. Die 1 schreiben wir in das Ergebnis.
• Wir rechnen zurück: 1 · 56 = 56.
• Wir subtrahieren: 67 - 56 = xi.
• Wir ziehen die nächste Stelle runter: Aus 11 wird damit 112.
• Die 56 geht in die 112 genau 2 mal rein. Wir schreiben die ii in das Ergebnis.
• Wir multiplizieren zurück: 2 · 56 = 112.
• Wir subtrahieren: 112 - 112 = 0.
• Wir ziehen mit 0 die nächste und letzte Stelle runter.
• Wie often geht die 56 in dice 0 rein? Gar nicht. Daher eine 0 ins das Ergebnis.
• Wir multiplizieren zurück: 0 · 56 = 0.
• Dice Subtraktion von 0 - 0 = 0 beendet dice Berechnung.

Beispiel ii:

Im zweiten Beispiel haben beide Zahlen ein Komma. Wir haben damit zwei Kommazahlen (sowohl Dividend als auch Divisor sind Dezimalzahlen). Berechnet werden soll 2,364 : 0,3.

Lösung:
Wir nehmen die Aufgabe

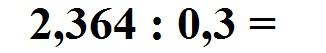
und multiplizieren diese mit 10. Dadurch fliegt bei der zweiten Zahl das Komma raus. Wir erhalten:

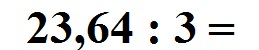
Wir dividieren nun wie dies oben auch schon gemacht wurde. Zunächst die Rechnung, im Anschluss wird die Berechnung kurz erklärt.

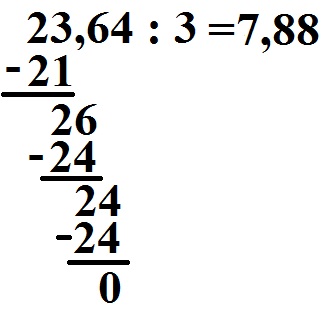
And so wurde gerechnet:

• Die two ist kleiner als die 3, daher starten wir mit 23.
• In dice 23 geht die 3 insgesamt 7 mal rein. Die seven schreiben wir in das Ergebnis.
• Wir multiplizieren zurück: 7 · 3 = 21.
• Wir subtrahieren 23 - 21 = 2.
• Wir ziehen dice half-dozen runter, aus ii wird 26.
• Die iii geht in dice 26 insgesamt 8 mal rein. Dice 8 kommt in das Ergebnis.
• Wir multiplizieren zurück: viii · 3 = 24.
• Wir subtrahieren: 26 - 24 = 2.
• Wir ziehen die four runter, aus 2 wird damit 24.
• Dice three geht in die 24 insgesamt viii mal rein. Die 8 kommt in das Ergebnis.
• Wir multiplizieren zurück: 8 · 3 = 24.
• Wir subtrahieren: 24 - 24 = 0. Rechnung komplett.

Aufgaben / Übungen schriftlich Dividieren mit Komma

Anzeigen:

Schriftlich Dividieren Video

Beispiele schriftliche Division mit Komma

Im Video werden viele Aufgaben zur schriftlichen Division mit Komma vorgerechnet. Dazu werden zunächst ganz einfache Beispiele gezeigt. Schritt für Schritt wird das Ergebnis (Quotient) ermittelt. Weitere Beispiele zeigen die schriftliche Sectionalisation mit Rest.

Nächstes Video »

Fragen mit Antworten schriftliche Division mit Komma

Source: https://www.gut-erklaert.de/mathematik/schriftlich-dividieren-komma-kommazahl.html

Posted by: ungercaresind.blogspot.com

Share this post